On a recent engagement, I came across Electronic Code Book (ECB) encrypted data. While there’s a plethora of documentation about performing bit flipping in ECB, I couldn’t find any decent writeups on how to perform adaptive chosen plaintext attacks to recover ciphertext.
In ECB mode, each block of plaintext is encrypted independently with the key as illustrated by the diagram below.
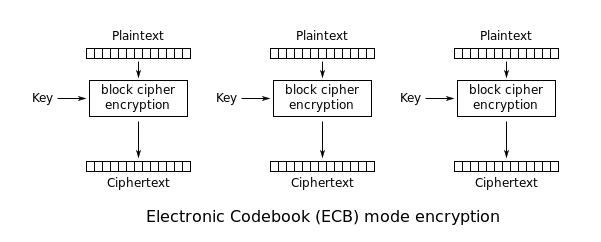(Source: Wikipedia)
Since each block of plaintext is encrypted with the key independently, identical blocks of plaintext will yield identical blocks of ciphertext. The classic and poignant example of this property is an encrypted image of the Linux mascot, Tux. Below are three images, the original Tux image, an ECB encrypted Tux and a CBC encrypted Tux. The ECB encrypted Tux leaves visible artifacts whereas the CBC encrypted Tux looks like random data.
Now that we’ve seen that ECB is bad, how do we break this?
Determining Block Size
The first step in attacking a block-based cipher is to determine the size of the block. Running our demo script, ecb_oracle.py, makes it pretty clear that our block size is 16 bytes.
./ecb_is_bad.py AAAA
pt: f o o b a r b a z 1 2 3 4 5 6 7 8 9 0 A A A A S e c r e t 4 2 X
ct: 0215a52009de7a0105517b91b3c7e4e8 da62a3b7a518c9befaa3875926feef6a
But in real-world applications, we can simple start sending specific lengths of plaintext into our cryptographic oracle (system that gives us ciphertext). In the example below, we’re sending 1 through 50 characters into our oracle.
for i in {1..50}; do echo $i; ./ecb_is_bad.py $(python -c "print 'A' * $i"); done
1
pt: f o o b a r b a z 1 2 3 4 5 6 7 8 9 0 A S e c r e t 4 2 X X X X
ct: 0215a52009de7a0105517b91b3c7e4e8 ada1ed6764f0e4292c850631aad51009
...
6
foobarbaz1234567890AAAAAASecret42XXXXXXXXXXXXXXX
ct: 0215a52009de7a0105517b91b3c7e4e8 a142fdb3b3eeac6638bce8d6fe4ff343 7cb6c28a1d4ece02b7cd85fe4966f2c8
...
22
foobarbaz1234567890AAAAAAAAAAAAAAAAAAAAAASecret42XXXXXXXXXXXXXXX
ct: 0215a52009de7a0105517b91b3c7e4e8 ebde81de5ef1d96ef9add35ff8cadfae 2e125f01887000dc649263c09070af17 7cb6c28a1d4ece02b7cd85fe4966f2c8
At 6 characters, our ciphertext increases by one block size and when we hit 22 it increases by another. By subtracting the input length between to block number increases, 6 and 22, we can find our block length (22 - 6 = 16 bytes).
Finding Our Offset
In real-world scenarios, we’ll most likely not have our chosen plaintext start as the first byte of a block, so we’ll need to calculate the offset. The offset can be found by prepending bytes in increasing length to block size * 2 of a static value until two consecutive blocks of ciphertext are found.
In the example below, our block size is 8 bytes and we control data starting at the last two bytes of the first block.
By adding characters to the beginning of our control data, we will eventually get two consecutive blocks of repeating ciphertext. In this example, we’re adding B’s to the beginning of our control data until we get two blocks of A’s.
Our example script can be attacked the exact same way:
./ecb_is_bad.py $(python -c "print 'B' * 1 + 'A' * 16 * 2")
pt: f o o b a r b a z 1 2 3 4 5 6 7 8 9 0 B A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A S e c r e t 4 2 X X X X
ct: 0215a52009de7a0105517b91b3c7e4e8 bcabfbc439aa11bf90089ba00ec44753 a8ab74fc58026896c6b988b0fa534291 f30e3f8b674cc2f84f356c30c0ede3cb
By increasing the number of offset bytes, we’ll end up with two consecutive blocks of ciphertext (a8ab74fc58026896c6b988b0fa534291) and have our number of offset bytes, 13.
./ecb_is_bad.py $(python -c "print 'B' * 13 + 'A' * 16 * 2")
pt: f o o b a r b a z 1 2 3 4 5 6 7 8 9 0 B B B B B B B B B B B B B A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A S e c r e t 4 2 X X X X X X X X
ct: 0215a52009de7a0105517b91b3c7e4e8 8931ed3815d4a0e7974c9437309be9ab a8ab74fc58026896c6b988b0fa534291 a8ab74fc58026896c6b988b0fa534291 7c1bd0bc4c6fce5d9f05dfc593ef7d1
Attack!!
Once we’ve determined our offset, we can start attacking the ciphertext. We’ll attack it by using a static value that’s block size - 1 in length. The last byte will get populated with a byte of unknown ciphertext as shown below and we record the resultant value as our reference value, 0fe034bf3bfb094ec51deee8384e8243.
./ecb_is_bad.py $(python -c "print 'B' * 13 + 'A' * 15")
pt: f o o b a r b a z 1 2 3 4 5 6 7 8 9 0 B B B B B B B B B B B B B A A A A A A A A A A A A A A A S e c r e t 4 2 X X X X X X X X X
ct: 0215a52009de7a0105517b91b3c7e4e8 8931ed3815d4a0e7974c9437309be9ab 0fe034bf3bfb094ec51deee8384e8243 c998c36f356089bf76b49646fa4e8946
We can now brute force the unknown byte by iterating though all possible values for the plaintext and comparing it to our reference value until we find a match. In the graphic below, the brute forced value is designated in red.
The following is pseudo code for brute forcing the byte of ciphertext.
for i in xrange(0, 255):
ct = oracle(offset + static + chr(i))
if ct[32:48] == target
print "Found %s" % chr(i)
To find the next value of unknown ciphertext, we can use a static value of block size - 2 so two bytes of the cipher text enter our controlled block (we already know the first).
./ecb_is_bad.py $(python -c "print 'B' * 13 + 'A' * 14")
pt: f o o b a r b a z 1 2 3 4 5 6 7 8 9 0 B B B B B B B B B B B B B A A A A A A A A A A A A A A S e c r e t 4 2 X X X X X X X X X X
ct: 0215a52009de7a0105517b91b3c7e4e8 8931ed3815d4a0e7974c9437309be9ab 17879752d4238d38c4a711596884cd75 20e48c85235cc96c075967e7abcda690
Now that we have our target ciphertext for the second unknown byte, 17879752d4238d38c4a711596884cd75, we can recover it by setting our payload to offset + static + found and brute forcing the unknown byte.
The following is pseudo code for brute forcing the second unknown byte of ciphertext:
for i in xrange(0, 255):
ct = oracle(offset + static + found + chr(i))
if ct[32:48] == target
print "Found %s" % chr(i)
Repeat this process until all of the plaintext is recovered for the secret.